Prompt: Given an m x n grid, how many unique paths are there with the start of the path being the top left corner and the end of the path being the bottom right corner?
Constraints:
~ 1 <= m, n <= 100
~ It’s guaranteed that the answer will be less than or equal to 2 * 109.
Example:
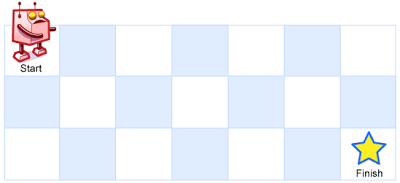
Input: m = 3, n = 7
Output: 28
Solution: The first two solutions would be DFS or BFS to find all the paths. Since the prompt only requests for the amount of paths rather than the specific paths, we can use a DP approach.
Given that each cell cares about the number of paths coming from it’s top and left neighbor, we can calculate the number of paths to a certain cell as the sum of the number of paths from its top neighbor and the number of paths from its left neighbor.
Note: paths(x, y) = paths(x - 1, y) + paths(x, y - 1)
The initial state of the grid should be 1s since each cell has 1 path in the beginning.