Prompt: There are n numbers of courses you need to take. Each course is represented by an integer id from 0 to n-1. There is also a list of prerequisites represented by an 2xn array, [[a₀,b₀],[a₁,b₁],[a₂,b₂],…,[a_n-1,b_n-1]], where b_i is a prerequisite of a_i. Given n number of courses, is it possible to take all courses?

Example:

Input: numCourses = 2, prerequisites = [[1,0]]
Output: true
Explanation: There are a total of 2 courses to take. 
To take course 1 you should have finished course 0. So it is possible.

Input: numCourses = 2, prerequisites = [[1,0],[0,1]]
Output: false
Explanation: There are a total of 2 courses to take. 
To take course 1 you should have finished course 0, and to take course 0 you should also have finished course 1. So it is impossible.

Solution: This is a dfs solution with backtracking. All of the prerequisites act like an directed edge for a graph. We need to look at the base cases of True and False, when you are able to take a course and when you are not able to take a course.

Let’s first look at the True case, when you are able to take a course.

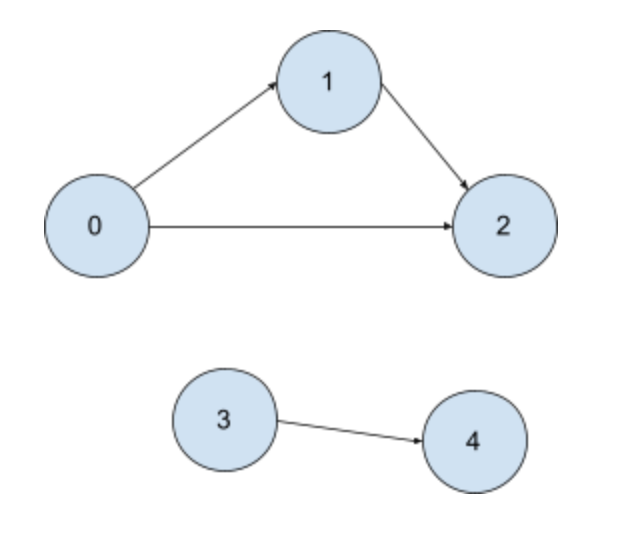
If prerequisites are [[0,1],[0,2],[1,2]], then

Graph = 
{
    0: [1,2]
    1: [2]
    2: [ ]
}

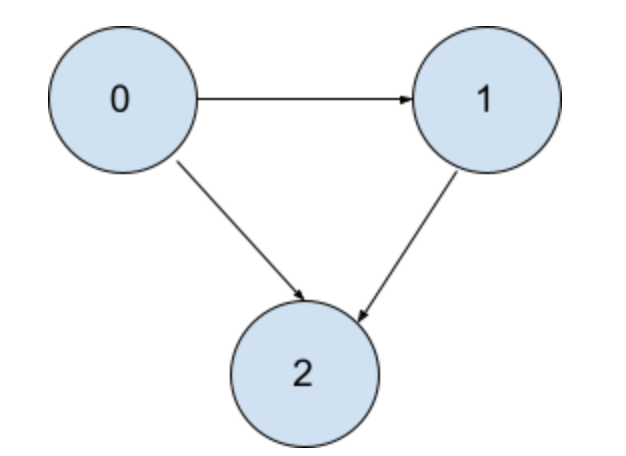
Notice that all courses that are free to take are empty lists. Course 2 is free to take since it doesn’t have any prerequisites. Hence, we can do a dfs from 0 to all the edges.

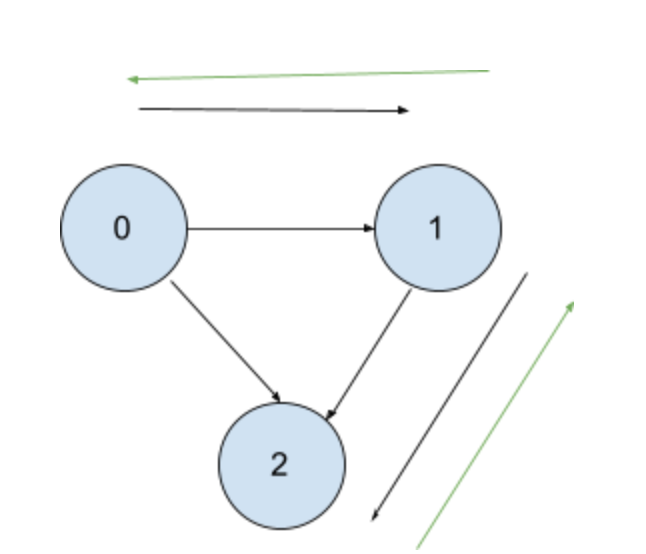
Let first dfs to the first prerequisite from 0, then dfs from 1 to 2. Finally, 2 doesn’t have a prerequisite so it returns True to 1 and to 0.

Since we don’t need to dfs from 0 to 1 and from 1 to 2, we can delete those edges. Then we can just repeat for all prerequisites.

Now that we have taken care of the True case. We have to see the False case, when you are not able to take the course.

If prerequisites are [[0,1],[1,0]], then

Graph: 
{
    0: [1]
    1: [0]
}

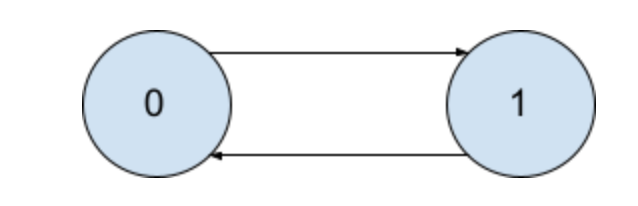
An example False case is there is a loop in a current path. How do you find a loop? We can have a set where it keeps all of its visited courses. If it visits a course twice, it means that there’s a loop in which the current combination of courses cannot be taken.

Pseudocode:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
DFS(course):
	If course is in visited set:
		Return False
	If graph[course] is empty:
		Return True
	
	Add course to visited set

	For each prerequisite in graph[course]:
		If not DFS(course):
			// if we can’t take one of the prerequisite courses, then we can’t take the current course
			Return False
	
	Remove course from visited set so other courses can visit it 
	Remove all prerequisites for the current course, you don’t need to check it anymore

	// if we can take all prerequisite courses, then we can take the current course
Return True

One more edge case that we have to think about is whether all nodes in the graph are connected or not. If the graph is not connected, all we have to do is to run the DFS function for all courses.

Example: